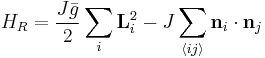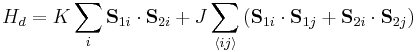Quantum rotor model

The quantum rotor model is a mathematical model for a quantum system. It can be visualized as an array of rotating electrons which behave as rigid rotors that interact through short-range dipole-dipole magnetic forces originating from their magnetic dipole moments (neglecting Coulomb forces). The model differs from similar spin-models such as the Ising model and the Heisenberg model in that it includes a term analogous to kinetic energy.

Although elementary quantum rotors do not exist in nature, the model can describe effective degrees of freedom for a system of sufficiently small number of closely coupled electrons in low-energy states.[1]

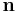Suppose the n-dimensional position (orientation) vector of the model at a given site i is \mathbf{n}. Then, we can define rotor momentum 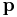\mathbf{p} by the commutation relation of components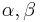 \alpha,\beta

[n_{\alpha},p_{\beta}]=i\delta_{\alpha\beta}

However, it is found convenient[1] to use rotor angular momentum operators 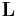\mathbf{L} defined (in 3 dimensions) by components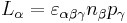 L_{\alpha}=\varepsilon_{\alpha\beta\gamma}n_{\beta}p_{\gamma}

Then, the magnetic interactions between the quantum rotors, and thus their energy states, can be described by the following Hamiltonian:

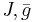H_R=\frac{J\bar{g}}{2}\sum_i\mathbf{L}_i^2-J\sum_{\langle ij\rangle}\mathbf{n}_i\cdot\mathbf{n}_j

where J,\bar{g} are constants.. The interaction sum is taken over nearest neighbors, as indicated by the angle brackets. For very small and very large 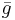\bar{g}, the Hamiltonian predicts two distinct configurations (ground states), namely "magnetically" ordered rotors and disordered or "paramagnetic" rotors, respectively.[1]

The interactions between the quantum rotors can be described by another (equivalent) Hamiltonian, which treats the rotors not as magnetic moments but as local electric currents.[2]

Properties

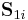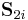One of the important features of the rotor model is the continuous O(N) symmetry, and hence the corresponding continuous symmetry breaking in the magnetically ordered state. In a system with two layers of Heisenberg spins \mathbf{S}_{1i} and \mathbf{S}_{2i}, the rotor model approximates the low-energy states of a Heisenberg antiferromagnet, with the Hamiltonian

H_d=K\sum_i\mathbf{S}_{1i}\cdot\mathbf{S}_{2i}%2BJ\sum_{\langle ij\rangle}\left(\mathbf{S}_{1i}\cdot\mathbf{S}_{1j}%2B\mathbf{S}_{2i}\cdot\mathbf{S}_{2j}\right)

using the correspondence 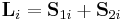\mathbf{L}_i=\mathbf{S}_{1i}%2B\mathbf{S}_{2i}[1]

The particular case of quantum rotor model which has the O(2) symmetry can be used to describe a superconducting array of Josephson junctions or the behavior of bosons in optical lattices.[3] Another specific case of O(3) symmetry is equivalent to a system of two layers (bilayer) of a quantum Heisenberg antiferromagnet; it can also describe double-layer quantum Hall ferromagnets.[3] It can also be shown that the phase transition for the two dimensional rotor model has the same universality class as that of antiferromagnetic Heisenberg spin models.[4]

See also

References

  1. ^ a b c d Sachdev, Subir (1999). Quantum Phase Transitions. Cambridge University Press. ISBN 978-0-521-00454-1. http://books.google.com/books?id=Ih_E05N5TZQC&printsec=frontcover. Retrieved 2010-07-10. 
  2. ^ Alet, Fabien; Erik S. Sørensen (2003). "Cluster Monte Carlo algorithm for the quantum rotor model". Phys. Rev. E 67 (1). arXiv:cond-mat/0211262. Bibcode 2003PhRvE..67a5701A. doi:10.1103/PhysRevE.67.015701. http://link.aps.org/doi/10.1103/PhysRevE.67.015701. Retrieved 24 July 2010. 
  3. ^ a b Vojta, Thomas; Sknepnek, Rastko (2006). "Quantum phase transitions of the diluted O(3) rotor model". arXiv:cond-mat/0606154. 
  4. ^ Sachdev, Subir (1995). "Quantum phase transitions in spins systems and the high temperature limit of continuum quantum field theories". arXiv:cond-mat/9508080.